Winkelsummen

[Heinrich Brucht]

Sehr geehrte Brettgäste,

seit Tagen peinigt mich mein Großneffe über den Elektropostkasten
mit folgender Aufgabenstellung:
Ich solle mir eine große Fläche vorstellen, die mit Fünfecken
vollständig überzogen ist.
Die Fünfecke liegen mit ihren Seiten aneinander und es stoßen
immer drei Ecken der Fünfecke zusammen.
Die Summe der Innenwinkel eines jeden Fünfecks ist 540 Grad.
Daraus folgt, daß ein Innenwinkel des Fünfecks im Durchschnitt
108 Grad hat. Bei einem symmetrischen Fünfeck hat jeder Innenwinkel
genau 108 Grad.
Wenn immer drei solche Winkel von 108 Grad zusammenstoßen,
so ergeben sie einen vollen Winkel. Dieser habe also 3 x 108 Grad,
das sind 324 Grad.
Nun behauptet aber die völlig übermotivierte gerade einmal 25 Jahre alte
Mathematiklehrerin, daß ein Vollwinkel sogar 360 Grad habe.
Das sind m.E. Aber ca. 11% zu viel !
Was mache ich nun mit der dummen Triene?
Gibt es Argumente oder brauch ich den Stock?

Betend
Heinrich Brucht

[Franz-Joseph von Schnabel]

Werter Herr Brucht,
dem Innenwinkel von 108° entspricht ein Außenwinkel von 72°.
Wundersamerweise ergeben sich, wenn man diese obskure Zahl 72, mit 5 multipliziert jener ominöse Wert von 360.
Sollte hier der Leibhaftige seine stinkenden Krallen im Spiel haben?
Um den Verbrauch an Fugendichtmasse zu minimieren, empfehle ich Ihnen jedoch die Nutzung von Vier- oder Sechsecken. Es sei denn Ihre Frau zupft gerne regelmäßig das Unkraut, welches aus den Zwischenräumen sprießt.
Das wissen selbst die fleißigen Bienen, welche scheinbar das von Ihnen erwähnte Weib an Intelligenz übertreffen.
Hinweisend,
Schnabel

[Heinrich Brucht]

Danke Herr Schnabel,

warum bin ich da nur nicht selber drauf gekommen?
Ich will es noch einmal zusammenfassen:

1.)
108 Grad + 72 Grad = 180 Grad , dies ist ein Halbkreis
zwei Halbkreise ergeben den Vollkreis, demnach 360 Grad
360 Grad = 2 x 108 Grad + 2 x 72 Grad

2.)
Legen wir jetzt die beiden Halbkreise zusammen, so ergibt sich
der Vollkreis, der aber auch gleichzeitig aus drei Innenwinkeln
der Fünfecke besteht.
Es ergibt sich: 2 x 72 Grad = 144 Grad
144 Grad wäre dann der dritte Innenwinkel im Vollkreis.
Er hat aber 108 Grad, weil 540/5 = 108 ist.
Die Ungenauigkeit ( 144 - 108 ) / 108 * 100 = 33,34% wäre nun
schon etwas deutlicher als nur o.g. 11%.

Fazit:
Möge mein Großneffe den Drachen jetzt vor die Wahl stellen,
entweder die 11% zu akzeptieren, oder beweisen zu müssen,
daß 144 = 108 ist.
Vielleciht kann man ja die Verhältnisse noch undrehen,
dann ergäbe sich:
entweder ( 144 - 108 ) / 144 * 100 = 25%
oder ( 360 - 324 ) / 360 = 10%
Mit 10% Ungenauigkeit sollten wir leben können,
so brauch ich den Stock wohl doch nicht.

Glücklich lächelnd
Heinrich Brucht

[Franz-Joseph von Schnabel]

Werter Herr Brucht,
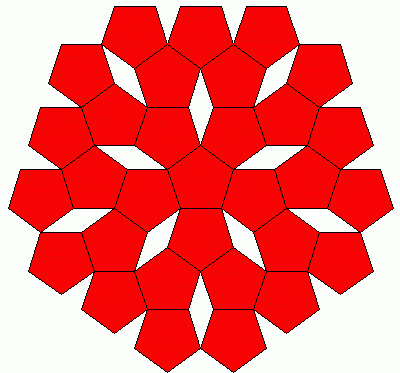
womöglich haben jene 11 v.H. auch mit diesen lustigen Rauten zu tun, welche sich bei Verlegung von Fünfecken ergeben?
Nachdenklich,
Schnabel

[Konrad Juckreiz]

Werte Herren,

144 ist immer gut, denn das ist nicht nur 2·72, sondern vor allem auch 12·12, also zahlenmystisch stehend für die zwölf Stämme Israels mal den zwölf Propheten, oder aber die Zahl der zwölf Apostel zum Quadrat.

Mehr dazu: 12².Bild

„Und ich hörte die Zahl der Versiegelten: Hundertvierundvierzigtausend aus allen Stämmen der Söhne Israels sollen das Siegel empfangen“ (Offenbarung 7,4)

Zitierend,

[Heinrich Brucht]

Meine Herren,

jetzt wird es nämlich interessant.

womöglich haben jene 11 v.H. auch mit diesen lustigen Rauten zu tun, welche sich bei Verlegung von Fünfecken ergeben?

Mein Großneffe hat einen Fußball fotografiert, ihn dann vergrößert ausgedruckt,
um der Lehrerin zu beweisen, daß man eine Fläche mit Fünfecken überziehen kann.
Selbst wenn diese nicht mehr symmetrisch wären, gilt immer noch,
- die Summe der Innenwinkel ist 540 Grad und
- es stoßen immer drei Fünfecke so aneinander, daß sie einen Vollkreis bilden.
Fraglich ist, ob der nun 324 Grad oder 360 Grad hat.

Wenn man das Bild von Herrn Schnabel ausdruckt, alle weißen Flächen herausschneidet
und die roten Flächen miteinander verbindet, so bekommt man auch ein kugeliges
Gebilde, welches fotografiert den Beweis wie der Fußball erbringen würde.
Man könnte die Oberfläche des Gebildes auch auf eine sehr große Ebene abbilden,
indem man es darauf in alle Richtingen rollt.

Mit dem Ergebnis, 360 ist näherungsweise 324 könnte ich somit leben.
Wie bringen wir das der Triene nur schonend bei?

Zufrieden
Heinrich Brucht

[Franz-Joseph von Schnabel]

Werter Herr Brucht,
eventuell könnte man die Fünfecke auch häckseln und in eine Tube füllen.
Im fernen Kairo pflegt man dergestalt Straßen zu pflastern.
Die Tube wiederum könnte man in einem Backofen auf die gewünschten 360 Grad erhitzen.
Hoffend, geholfen zu haben,
Schnabel

[Alberto Bonappetito]

Dämlack Brucht

Ein Fußball besteht aus Fünfecken und Sechsecken, wie man auf dem Bild unten erkennen kann.


Den Fußball des Nachbarsjungen zerstechend, nachdem dieser erneut in meinem Garten landete
Alberto Bonappetito

[Heinrich Brucht]

Meine Herren,

da meine mathematische Bestform jetzt über 30 Jahre her ist,
will ich mal in kleinen Schritten weiter machen.

Die Innenwinkelsumme beim Sechseck ist 720 Grad,
demzufolge hat ein Innenwinkel im Durchschnitt 120 Grad,
beim symmetrischen Sechseck sind es genau 120 Grad.

Nun stoßen beim Fußball 2 x 120 Grad + 1 x 108 Grad zusammen
und bilden den Vollkreis mit 348 Grad. Damit wäre die Abweichung
zu 360 Grad nur noch ca. 3,4%.

Würde man eine Fläche nur mit Sechsecken überziehen, so ergibt
sich seltsamerweise überhaupt keine Abweichung mehr.

Überziehen wir die Fläche mit Siebenecken, so ergibt sich:
Die Innenwinkelsumme beträgt 900 Grad.
Ein Innenwinkel hat durchschnittlich 128,57 Grad.
Stoßen drei solche Winkel zusammen, so haben die zusammen
ca. 385, 71 Grad.
Die Abweichung zu 360 Grad beträgt ca. 7,14%

Mein vorläufiges Fazit:
Die Ungenauigkeiten liegen meist unter 11%, womit wir prinzipiell leben könnten.
In anderen Bereichen ( z.B. Projektentwicklung, Bauwesen ) liegen die Ungenauigkeiten
wesentlich höher.
Dies möge mein Großneffe der Lehrerin per Elektropost mitteilen. Montags geht er mal
nicht in die Schule. Er wird mir im Holz helfen wollen.

Rundum zufrieden
Heinrich Brucht.

[Jeremias Töfte]

Trunkenbold Brucht!

Seit geraumer Zeit fallen mir Ihre Beiträge auf, die überhaupt nicht zu den Themen passen.
Bitte unterlassen Sie dies in diesem Forum.

Abgesehen davon ist Ihr mathematischer Fehler der folgende:
Die Innenwinkel müssen im Durchschnitt, aber nicht exakt 108° groß sein.
Betrachtet man nun zum Beispiel ein Fünfeck, bei denen ein Winkel 180° und die anderen 90° groß sind, so ist dieses äquivalent zu einem Rechteck, das einen zusätzlichen Eckpunkt auf einer Kante besitzt.
Mit solchen ließe sich eine unendliche Fläche parkettieren.

Hinweisend,
Töfte

[Franz-Joseph von Schnabel]

Werter Herr Töfte,
ich möchte Sie bitten die Formen der Höflichkeit einzuhalten und die Brettregeln zu beachten.
Dennoch ist Ihrem Ansatz eine gewisse Genialität nicht abzusprechen.
Ließe sich so doch jedes beliebige n-Eck auf ein Viereck zurückführen. Wenn man nun den Kreis als solches mit n=Unendlich definiert, ist Ihnen die Lösung eines uralten Problems geglückt: Die Quadratur des Kreises!
Die Schaffung eines Nobelpreises für Mathematik anregend,
Schnabel

[Stephan Schmid]

Werte Herren

auf DuRöhre gibt es einen guten Streifen, der die Qadratur des Kreises wunderschön aufzeigt.
http://www.youtube.com/watch?v=UDDqjPeHj6s

Eventuell hilft dies Personen, die sich unter dem Zahlensalat nichts vorstellen können.

Ein schönes Wochenende wünschend
Stephan Schmid

[Heinrich Brucht]

Meine Herren,

die Idee von Herrn Töfte, ein Fünfeck auf ein Viereck zureduzieren,
finde auch ich sehr annehmbar.
Leider kam sie etwas zu spät und ich hab derweil meine eigene
Lösungsidee entwickelt.
Ich hab meinen Großneffen mal eine Woche von der Schule genommen,
so daß er sich bei der Waldarbeit von seiner "Ausgebranntheit"
erholen konnte.
Die Lehrerin hat eingelenkt.

Morgen nach dem Gottesdinst will ich einen nicht unerheblichen Betrag spenden.

Gut gelaunt
Heinrich Brucht

[Jeremias Töfte]

Werter Herr Brucht,

noch eine Frage: Was hat eine derartige Aufgabe in diesem Brett zu suchen?
Dafür gibt es meines Wissens einen Ab-Thema-Faden.

Verwundert,
Töfte

[Heinrich Brucht]

Herr Töfte,

prinzipiell kann ich Ihre Sorge um die Brettstruktur verstehen.
Als ich den Faden gestartet hab, glaubte ich jedoch, ich müsse eine
sinnvolle Methode suchen, um die abtrünnige Lehrerin zu bekehren.
Prinzipiell hätte ich den Anlaß des Streites ( die blödsinnige Aufgabe )
auch weglassen können.

Verallgemeinert hätte meine Fragestellung auch lauten können:

Was ist zu tun, wenn sich ein mächtiges teuflisches Lehrerweib
an der Seele eines töften Christenkindes vergreift?

Mögliche Optionen:
- kluge Argumente auf Grundlage der Bibel,
- rechtsstaaatliche Mittel,
- sofortige Züchtigung.

Vielleicht will ich das jetzt nochmals überdenken.

Herzlichen Dank für den Hinweis, Herr Töfte.
Heinrich Brucht